POTENTIEL ET FONCTIONS HARMONIQUES

POTENTIEL ET FONCTIONS HARMONIQUES

La théorie du potentiel, directement issue de l’électrostatique, est une source d’inspiration extrêmement riche en analyse. Si, au début du XIX^e siècle, on connaissait déjà l’équation de Laplace, la fonction de Green et l’intégrale de Poisson dans la boule, ce n’est vraiment qu’avec C. F. Gauss (1840) que sont posés et résolus, bien qu’imparfaitement, les grands problèmes de la théorie. Les idées de ce dernier sont si exemplaires qu’elles sont encore utilisées à l’heure actuelle, et il fallut attendre Frostman (1935) pour que le travail de Gauss fût amélioré en précision et en rigueur par l’introduction des outils nouveaux que s’était entre-temps forgés l’analyse.

On commencera par exposer les éléments fondamentaux qui permettront d’énoncer les problèmes et les principes les plus importants et les plus spécifiques de la théorie du potentiel: théorèmes de convergence, principe de domination, problème du balayage (cela afin d’arriver de la façon la plus directe à des résultats suffisamment précis). On se limitera ainsi au cas d’un ouvert borné, et on omettra de parler de «topologie fine» et de tout un chapitre de la théorie fine du potentiel. On ne pourra pas, non plus, parler des théories plus spéciales, comme par exemple la théorie très importante des potentiels besséliens d’Aronszajn et Smith. On envisagera quelques-unes des théories axiomatiques ou dérivées, issues de la théorie du potentiel, en mettant l’accent sur le lien avec la théorie des probabilités et celle des équations aux dérivées partielles: c’est là un centre de recherche important.

Le sujet est immense et la théorie du potentiel occupe une position centrale en analyse. En étudiant l’existence d’une solution du problème de Dirichlet, I. Fredholm considéra l’équation intégrale qui porte son nom; c’est aussi à l’occasion de l’étude d’un critère de polyharmonicité que Laurent Schwartz a été amené à définir les distributions. Les problèmes de Dirichlet et de Neumann sont également des problèmes fondamentaux de la théorie des équations aux dérivées partielles. Enfin, la théorie de la capacité peut être considérée comme un chapitre important de la théorie de la mesure (ou vice versa), et le théorème de représentation intégrale de Choquet est tout aussi surprenant par sa simplicité que par sa profondeur et son efficacité.

1. Fonctions surharmoniques et potentiels

Pour tout ensemble A de Rⁿ , on note 煉A sa frontière topologique et A 漣 son adhérence. B(x , r ) désigne une boule ouverte de centre x et de rayon r .

La mesure de Lebesgue est notée dx et on entend par fonction réelle une fonction à valeurs réelles prenant éventuellement les valeurs + 秊 et 漣 秊.

Fonctions surharmoniques et harmoniques

Une fonction réelle u définie dans un ouvert 諸 de Rⁿ , n 閭 2, est dite hyperharmonique si elle est semi-continue inférieurement et 礪 漣 秊, et si, pour tout x 捻 諸 et pour toute boule B = B(x , r ), B 漣 說 諸, on a:

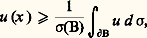où d 靖 désigne la mesure superficielle de la boule et 靖(B) l’aire de la boule B. On exprime cette dernière condition en disant que u majore sa moyenne sur toute boule.

De manière analogue, u est dite hypoharmonique si elle est semi-continue supérieurement et 麗 + 秊 et si, avec les notations précédentes,

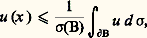pour B 漣 說 諸.

Le module ou le logarithme du module d’une fonction holomorphe de la variable complexe z est hypoharmonique.

On dit qu’une fonction f définie dans un ouvert 諸 de Rⁿ vérifie le «principe du minimum» si, pour tout ouvert 嗀, avec 嗀 漣 compact 說 諸, la condition:

pour tout x 捻 煉 嗀, entraîne f 閭 dans 嗀.

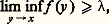Propriétés des fonctions hyperharmoniques

1. Dans un ouvert 諸, une fonction hyperharmonique ne peut atteindre un minimum en un point de 諸 sans être constante au voisinage. Cela entraîne que les fonctions hyperharmoniques dans un ouvert vérifient le principe du minimum.

2. L’ensemble des fonctions hyperharmoniques forme un cône convexe qui est stable par enveloppe inférieure finie.

3. L’enveloppe supérieure d’un ensemble filtrant croissant de fonctions hyperharmoniques est hyperharmonique.

4. Dans un domaine 諸 說 Rⁿ , une fonction hyperharmonique finie en un point est finie presque partout. Elle est alors dite surharmonique.

5. Une fonction localement surharmonique est surharmonique.

6. Si s est surharmonique dans un ouvert 諸 說 Rⁿ , pour tout p et tout compact K 說 諸, il existe une suite croissantesⁿ de fonctions surharmoniques p fois continûment différentiables dans un ouvert 嗀 contenant K, telle que:

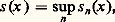pour tout x 捻 嗀.

Les propriétés 2, 3 et 4 sont évidentes. Les propriétés 1, 5 et 6, plus difficiles, sont fondamentales.

Une fonction u telle que u et 漣 u soient surharmoniques est dite harmonique. Elle est donc finie, continue et égale à sa moyenne en tout point.

Propriétés des fonctions harmoniques

1. Une fonction harmonique u dans un ouvert 諸 說 Rⁿ ne peut avoir un maximum ou un minimum en un point de 諸 sans être constante au voisinage.

2. Les fonctions harmoniques sont indéfiniment dérivables.

Il suffit pour le voir de faire le produit de convolution de u harmonique dans un ouvert 諸 avec la fonction indéfiniment dérivable 﨏 définie par: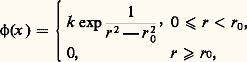

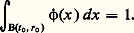r = 瑩x 漣 t ⁰ 瑩, pour B(t ⁰, r ⁰) 說 諸, la constante k étant choisie de telle sorte que:

En écrivant u sous le signe 咽 en fonction de sa valeur moyenne et en intervertissant l’ordre des intégrations, on vérifie que la fonction 﨏 u , définie par:

est indéfiniment dérivable en t ⁰, et vaut u (t ) au voisinage de t ⁰.

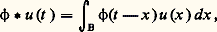3. Une fonction u est harmonique dans 諸 si et seulement si, pour toute boule B 說 B 漣 說 諸, on a, en désignant par du/dn la dérivée normale de u sur 煉B,

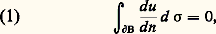ce qu’on exprime en disant que le flux sortant est nul.

En effet, si u est harmonique, la moyenne de u sur B(t ⁰, r ) ne dépend pas de r et, en dérivant sous le signe 咽, on obtient (1). Inversement, l’intégration de (1) en r montre que u vaut sa moyenne.

4. Une fonction u est harmonique si et seulement si elle vérifie u = 0 où désigne le laplacien.

Cela résulte immédiatement de la formule de Green:

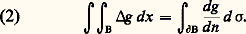Ainsi, la partie réelle d’une fonction holomorphe est harmonique (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe, chap. 3).

5. Une fonction harmonique est analytique.

6. Dans le plan, l’inversion et les transformations conformes conservent l’harmonicité. Dans Rⁿ , n 閭 3, l’inversion ne conserve pas l’harmonicité: si une inversion I^{x 0} de centre x ⁰ transforme x en x , u harmonique se transforme en V tel que V(x ) = u (x ), alors:

est harmonique. La fonction h s’appelle la transformée de Kelvin de u .

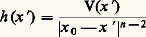La transformation de Kelvin (inversion dans le plan) conserve également la surharmonicité. Ajoutons aussi qu’une fonction s surharmonique vérifie s 諒 0 au sens des distributions. Cela se voit facilement pour s de classe 暈² à l’aide d’un développement limité à l’ordre 2. On passe au cas général en utilisant une suite croissante d’après la propriété 6 des fonctions surharmoniques.

Potentiel newtonien et logarithmique

En écrivant le laplacien en coordonnées polaires et en cherchant des solutions de u = 0 qui ne sont fonction que de la distance r à l’origine, on trouve les fonctions:

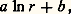pour n = 2, et les fonctions: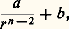

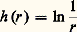pour n 閭 3, a et b étant des constantes arbitraires.

On introduit alors la fonction harmonique fondamentale h (r ). Dans le plan:

s’appelle noyau logarithmique . Dans l’espace Rⁿ , n 閭 3,

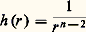est le noyau newtonien. La fonction h est surharmonique et harmonique en dehors de l’origine.

Si 猪 est une mesure à support compact (par exemple), la fonction:

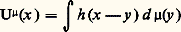s’appelle potentiel logarithmique ou newtonien selon que l’on se place dans le plan ou l’espace. On parlera aussi de potentiel classique si l’on ne veut pas préciser: il faut noter que ce potentiel n’est pas partout défini. En pensant à une charge électrique répartie (par exemple continûment) avec une densité 福 sur une surface , on a:

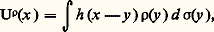où d 靖 représente la mesure d’aire de la surface. C’est pourquoi on utilise un langage imagé en disant que la mesure 猪 représente la charge ou les masses du potentiel. Par dérivation sous le signe somme, on vérifie facilement que U size=1^猪 est harmonique en dehors du support de 猪. Il faut aussi savoir que, si 猪 est positive, U size=1^猪 est surharmonique.

Il y a une différence essentielle entre le cas du plan et celui de l’espace, qui provient de la différence de comportement des noyaux à l’infini: toute fonction surharmonique positive dans R² tout entier est constante.

Intégrale de Poisson et problème de Dirichlet

La formule de Poisson dans la boule B = B(O, R):

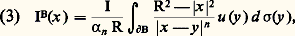où 見ⁿ désigne l’aire de la boule de rayon 1, peut s’obtenir de diverses manières. La plus simple consiste à utiliser la transformation de Kelvin de la façon suivante: Si x désigne l’inverse de x dans l’inversion de centre O et de puissance R², on effectue la transformation de Kelvin de centre x qui transforme x en O et qui conserve 煉B(O, R). La fonction u (y ) devient alors h (y ), et on écrit que la valeur en O est la moyenne de h sur 煉B. En transformant cette intégrale sur h en intégrale relative à u , on obtient la relation cherchée.

La formule de Poisson permet de résoudre le problème de Dirichlet dans le cas de la boule: Si f est une fonction donnée finie continue sur 煉B, alors I^{f B} est un prolongement continu de f dans B 漣, harmonique dans B.

Inégalités de Harnack et familles de fonctions harmoniques

Une majoration suivie d’une minoration de (3) donne, pour u 礪 0 harmonique dans B(O, R), les deux formules suivantes:

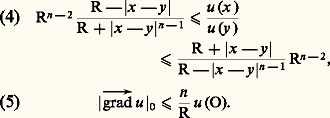On en déduit immédiatement:

Théorème 1 : Toute famille 杻 localement bornée de fonctions harmoniques dans un ouvert 諸 est équicontinue en tout point de 諸.

Corollaire 2 (Ascoli) : La convergence simple d’une suiteuⁿ localement bornée entraîne la convergence uniforme locale vers une fonction harmonique. Si 諸 est connexe, il suffit, grâce à l’analyticité, queuⁿ converge simplement au voisinage d’un point.

De toute suiteuⁿ on peut extraire une suiteu^np convergeant uniformément localement vers une fonction harmonique.

L’inégalité (5) montre encore que la convergence uniforme locale de u entraîne celle des dérivées successives.

En partant de (4) ou du théorème précédent, on peut montrer facilement les deux propriétés suivantes, d’ailleurs équivalentes dans un domaine 諸:

a ) Pour tout K compact inclus dans 諸, il existe une constante k 礪 0 dépendant seulement de K et de 諸 telle que, pour toute fonction harmonique u 礪 0 dans 諸, on ait les inégalités de Harnack:

quels que soient x , y 捻 K.

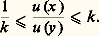b ) Pour toute famille (uⁱ ) filtrante croissante de fonctions harmoniques dans 諸, si sup uⁱ est finie en un point, sup uⁱ est finie et harmonique dans 諸.

L’équicontinuité jointe à l’inégalité de Harnack permet d’énoncer que toute famille (uⁱ ) de fonctions harmoniques, localement bornée inférieurement dans un domaine, forme une famille normale de Montel; autrement dit: de toute suite (uⁿ ) 說 (uⁱ ) on peut extraire une suite convergeant vers + 秊 ou vers une fonction harmonique (uniformément localement).

Théorème de représentation de Riesz

Soit y un point de B(x ⁰, R). On appelle fonction de Green ou bien noyau de Green de la boule B(x ⁰, R) relative au pôle y la fonction:

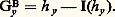où I(h^y ) est l’intégrale de Poisson dans B de la restriction de h^y à 煉B.

Si y ¹ est l’inverse de y dans l’inversion de centre x ⁰ qui conserve 煉B, on a explicitement:

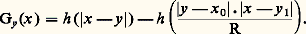La fonction G^y , surharmonique positive dans B, est harmonique en dehors de y , s’annule sur 煉B et vérifie la propriété de symétrie G^y (x ) = G^x (y ).

On définirait plus généralement la fonction de Green d’un ouvert borné 諸 en posant:

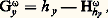où H size=1^諸by désigne la solution généralisée du problème de Dirichlet avec pour donnée frontière la trace de h^y sur 煉 諸. La seule différence provient de ce que G^y ne s’annule pas partout à la frontière.

Si 猪 est une mesure positive, la fonction:

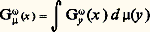est appelée potentiel de Green, potentiel pur ou simplement potentiel. C’est une fonction hyperharmonique positive dans 諸.

Si le potentiel U size=1^猪 est deux fois continûment différentiable et 猪 = 福 dx , avec 福 continue, on obtient, à l’aide de la formule de Green, l’équation de Poisson:

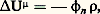où 﨏ⁿ est un coefficient numérique dépendant de n .

Plus généralement, si T est une distribution à support compact, U^T se définit encore comme la distribution h T, et on a encore au sens des distributions:

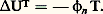L’équation de Poisson permet de connaître la charge quand on connaît le potentiel et permet de démontrer le théorème suivant.

Théorème 3 (théorème de représentation de Riesz) : Si V, surharmonique dans un ouvert borné 諸, admet une minorante harmonique dans 諸, on a:

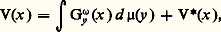où V est la plus grande minorante harmonique de V et 猪 la mesure positive 漣 V/ 﨏ⁿ .

L’existence d’une plus grande minorante harmonique résulte de la proposition suivante.

Proposition 4 : Si 杻 est la famille des fonctions sous-harmoniques minorant la fonction surharmonique V, alors h = sup 杻 est harmonique.

La fonction h est alors la plus grande minorante harmonique de V. Cela se démontre en utilisant le fait que l’on peut remplacer s sous-harmonique dans 諸 par la fonction s égale à I^{s B} dans la boule B 說 B 漣 說 諸 et égale à s ailleurs. De ce fait, s 諒 s , et s est encore sous-harmonique. On remarque que 杻 est filtrante croissante. Si 杻 désigne la famille des fonctions s quand s parcourt 杻 pour B donné, on voit que sup 杻 = sup 杻 est harmonique dans B (théorème de convergence pour les fonctions harmoniques); B étant arbitraire, h est harmonique (critère local).

Notons qu’un potentiel est donc caractérisé comme une fonction surharmonique positive dont la plus grande minorante harmonique est nulle.

2. Théorèmes et principes fondamentaux

Balayage

On appelle S-fonction une fonction u localement bornée inférieurement qui vérifie, pour toute boule B(x , R), la relation:

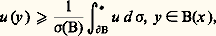où d 靖 est la mesure-aire de 煉B et 咽 l’intégrale supérieure.

L’utilité de ces fonctions provient de ce que l’enveloppe inférieure d’une famille de S-fonctions localement bornée inférieurement est une S-fonction et que la régularisée semi-continue inférieurement d’une S-fonction est hyperharmonique.

Soit 諸 un ouvert borné de Rⁿ , E 說 諸, et 﨏 une fonction 閭 0 sur E. On note (R size=1^﨏E) size=1^諸 ou R size=1^﨏E l’enveloppe inférieure des fonctions v hyperharmoniques 閭 0 dans 諸 qui majorent 﨏 sur E. La fonction R size=1^﨏E s’appelle la réduite de 﨏 sur E et est une S-fonction; c’est une fonction croissante de E, positivement homogène et sous-additive en 﨏.

La proposition 4 montre que R size=1^﨏E est harmonique, ou égale à + 秊, en dehors de E.

Si 﨏 est la trace d’une fonction surharmonique v 閭 0, la régularisée R^vE, alors surharmonique, est appelée la balayée de v sur E. Si E est suffisamment régulier (une boule, par exemple), la balayée vaut v sur E; et, si v est un potentiel G size=1^猪, la balayée, majorée par G size=1^猪, est encore un potentiel qui vaut G size=1^猪 sur E. On peut donc écrire:

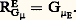On dit que 猪^E est la balayée de 猪 sur E et que 猪^E engendre le même potentiel que G size=1^猪 sur E. On dit de façon imagée que l’on a balayé les masses sur E. C’est en fait ce qui se passe: si E est toujours un compact suffisamment régulier, 猪^E est alors constituée des masses de 猪 portées par E, auxquelles viennent s’ajouter les masses de 猪 qui n’étaient pas portées par E. Une étude approfondie donne un résultat plus précis pour E quelconque.

Principe de domination

Plusieurs formes plus ou moins fortes du principe de domination peuvent être données, dont celle-ci: Si, dans un ouvert 諸, une fonction surharmonique majore un potentiel G size=1^猪, localement borné sur le support de 猪, elle le majore partout. Si G size=1^猪 était continu, il ne s’agirait de rien d’autre que du principe du minimum.

Capacité

Soit K un compact d’un ouvert borné 諸 de Rⁿ . On appelle potentiel capacitaire de K la balayée R¹K de 1 sur K. La mesure qui l’engendre s’appelle la mesure capacitaire et 猪(K) est la capacité de K, notée 暈(K). Grâce au principe de domination, on voit que R^1K est le plus grand potentiel majoré par 1 dans 諸 ayant une masse associée 閭 0 portée par K. Ce résultat donne la formule plus connue:

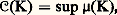où la borne supérieure est prise pour l’ensemble de toutes les mesures positives 猪 portées par K telles que G size=1^猪 諒 1 sur K.

La capacité 暈 est une fonction d’ensemble définie sur les compacts de 諸 et telle que:

1. La fonction 暈 est une fonction croissante:

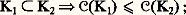2. Si (Kⁿ ) est une suite décroissante de compacts, d’intersection K 歷, on a:

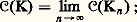on dit que 暈 descend sur les compacts;

3. On a la propriété de sous-additivité forte. Pour tous compacts K¹ et K², on a:

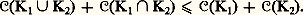On définit aussi la capacité intérieure 暈(E) et la capacité extérieure 暈(E) d’un ensemble quelconque E par:

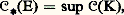où la borne supérieure est prise pour K parcourant l’ensemble des compacts contenus dans E, et:

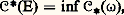où la borne inférieure est prise pour 諸 parcourant l’ensemble des ouverts contenant E.

On montre que, pour E relativement compact dans 諸, 暈(E) est encore la masse totale de la mesure associée à R^1E.

La fonction 暈 est croissante, descend sur les compacts et monte sur les ensembles quelconques; cela signifie que, si (Eⁿ ) est une suite croissante d’ensembles quelconques, on a:

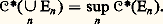Ensembles exceptionnels

Il existe des ensembles de capacité strictement positive, qui sont très petits. Par exemple, dans le plan, l’ensemble fermé de Cantor sur le segment [0, 1] est de capacité strictement positive alors qu’il est non seulement de mesure nulle (dans R²), mais de mesure linéaire nulle. La capacité mesure donc de façon très fine la petitesse des ensembles. On verra qu’elle est parfaitement adaptée à la mesure des ensembles exceptionnels de la théorie du potentiel.

On dit qu’une propriété est vraie quasi partout (on note en abrégé q.p.) si elle est vraie en dehors d’un ensemble de capacité extérieure nulle. Un ensemble P est dit polaire dans un ouvert borné s’il existe un potentiel G size=1^猪 fini en un point et infini sur P (contrairement aux apparences, cela ne dépend pas de 諸 borné).

H. Cartan a montré qu’il y avait identité entre ensemble polaire et ensemble de capacité extérieure nulle dans un ouvert borné. Il a aussi démontré le théorème suivant, qui avait été obtenu précédemment par M. Brelot pour la capacité intérieure. Ce théorème est la clef de toutes les études fines de la théorie.

Théorème 5 (théorème de Cartan-Brelot) : L’enveloppe inférieure d’une famille (vⁱ ) localement bornée inférieurement de fonctions surharmoniques dans un ouvert 諸 de Rⁿ diffère de sa régularisée semi-continue inférieurement d’un ensemble polaire. Cela permet de préciser pour un ensemble E quelconque que R^{v E}, pour v surharmonique 閭 0, est égale q.p. à v sur E.

Problème de Dirichlet généralisé et effilement

Soit 諸 un ouvert borné et f une donnée frontière (finie ou non). On considère la famille 淋 des fonctions hyperharmoniques v telles que:

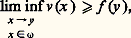pour tout y 捻 煉 諸, cette limite inférieure étant 礪 漣 秊 partout sur 煉 諸. On définit:

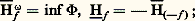on a alors:

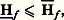et H^f (x ) est une fonction positivement homogène et sous-additive de f . Si on a 漣H^f = H^f = H^f , on dit que f est résolutive et H^f est alors la solution généralisée du problème de Dirichlet. Cette construction est due à Perron. Pour sa part, N. Wiener montra que f finie continue était résolutive et qu’ainsi f 料 H^f (x ) définissait une mesure de Radon positive 福^x size=1^諸 appelée mesure harmonique. Brelot montra alors que pour qu’une fonction f , définie sur 煉 諸, soit résolutive, il faut et il suffit qu’elle soit 福^x size=1^諸 intégrable; cela ne dépend pas de x 捻 諸.

Un point frontière x ⁰ 捻 煉 諸 est dit régulier si, pour toute f finie continue sur 煉 諸, on a:

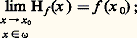si tout point frontière est régulier, on dit que 諸 est régulier . C’est le cas de la boule.

On dit qu’un ensemble E est effilé en un point x ⁰ 殮 E si x ⁰ n’est pas adhérent à E ou s’il existe une fonction surharmonique v au voisinage de E telle que:

si x ⁰ 捻 E, on dit encore que E est effilé en x ⁰ si E 漣x ⁰ est effilé en x ⁰.

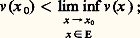On montre alors qu’il existe un potentiel fini continu P dans 諸 (ouvert borné) tel que, pour tout E 說 諸, l’ensemble des points d’effilement de E coïncide avec l’ensemble des points x pour lesquels on a:

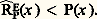On en déduit, d’après le théorème 5, que l’ensemble des points de E, où E est effilé, est polaire (ou de capacité extérieure nulle). Si 諸 est un ouvert borné, on montre que x ⁰ est régulier pour 諸 si et seulement si son complémentaire est non effilé en x .

Il s’ensuit que l’ensemble des points irréguliers forme un ensemble polaire.

Fonctions harmoniques positives et frontières de Martin

Toute fonction harmonique positive u dans la boule B(O,R) s’écrit:

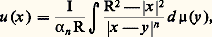où 猪 est une certaine mesure 閭 0 sur 煉B. Citons aussi le théorème de Fatou qui affirme que toute fonction harmonique positive dans la boule B admet une limite angulaire en presque tout point x 捻 煉B.

En 1941, R. S. Martin, afin de généraliser cette représentation intégrale au cas d’un ouvert borné, introduisit la fonction de Green normalisée :

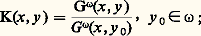il montra l’existence d’un espace compact 諸, unique à un homéomorphisme près, tel que 諸 = 諸 漣 et prouva que la famille des fonctions x 料 K(x , y ) se prolonge continûment à 臨 = 諸 漣 諸 et sépare 臨. On appelle 臨¹ l’ensemble des points X 捻 臨 tels que la fonction prolongée correspondante K(X, y ) soit minimale, c’est-à-dire telle que toute fonction harmonique 礪 0 majorée par K(X, y ) lui soit proportionnelle. À toute fonction harmonique h 閭 0 dans 諸 correspond alors sur 臨 une mesure unique 猪^h 閭 0 portée par 臨¹ telle que:

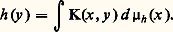Brelot a résolu un problème de Dirichlet avec donnée frontière sur 臨. On peut alors faire une étude du comportement à la frontière des fonctions harmoniques positives, grâce à l’introduction de l’effilement minimal (Naïm), et généraliser, à l’aide de la topologie fine, le résultat de Fatou sur les limites angulaires dans le cas de la boule (J. L. Doob).

3. Liens avec l’analyse fonctionnelle

Énergie

La physique élémentaire nous apprend que l’unique charge électrique q du potentiel capacitaire V d’un conducteur donne un état d’équilibre et correspond à un minimum de l’énergie:

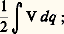on dit que V est un potentiel d’équilibre. C’est cette idée qui conduisit Gauss, en 1840, à considérer l’intégrale:

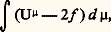où U size=1^猪 est le potentiel newtonien d’une mesure 猪 donnée par une densité sur une surface rendant minimum l’intégrale. Or cela n’est vrai qu’avec des restrictions qui furent éclaircies par Frostman en 1935. Ce sont, au fond, les idées de Gauss qui sont à l’origine du travail de Cartan sur l’énergie dont il est question ci-dessous.

Dans Rⁿ , n 閭 3, avec le noyau newtonien, on appelle énergie mutuelle de deux mesures 猪 et 益 閭 0 la quantité:

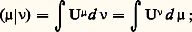pour toute mesure 猪, on appelle énergie de 猪 le nombre 瑩 猪 瑩^e = 連( 猪| 猪) et, à l’aide de l’inégalité fondamentale (non évidente),

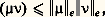il est facile de voir que 猪 料 瑩 猪 瑩^e est une semi-norme et, par suite, que l’ensemble des mesures positives ou nulles d’énergie finie est un cône convexe 劉⁺.

On considère ensuite l’espace vectoriel 劉 = 劉⁺ 漣 劉⁺ et on prolonge de façon standard la semi-norme à 劉. L’inégalité fondamentale est encore vérifiée et la semi-norme prolongée est encore une semi-norme sur 劉.

Principaux théorèmes

Théorème 6 (principe de l’énergie de Frostman) : La semi-norme 瑩 猪 瑩^e est une norme sur 劉.

Corollaire 7 : L’espace 劉 est un espace préhilbertien muni du produit scalaire ( 猪| 益).

Théorème 8 (principe de domination ou principe du maximum de Cartan) : Soit 猪 捻 劉 et v surharmonique positive majorant U size=1^猪 sur un support restreint de u (c’est-à-dire un ensemble dont le complémentaire est de 猪-mesure nulle); alors v majore U size=1^猪 partout dans Rⁿ .

Théorème fondamental (Cartan) : Le cône convexe 劉⁺ est complet dans 劉.

On utilise pour la démonstration de ce théorème le théorème de représentation de Riesz (théorème 3). Un exemple de Cartan montre que 劉 n’est pas complet.

Si K est un compact de Rⁿ , on peut montrer que l’ensemble 杻^K des mesures 捻 劉⁺ portées par K est un cône convexe complet de 劉; on obtient (9) et (10).

Théorème 9 (du balayage) : Soit 猪 捻 劉⁺. La projection 猪^K de 猪 sur 杻^K est caractérisée comme la seule mesure 閭 0 sur K telle que, d’une part, on a partout l’inégalité:

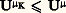et, d’autre part, pour toute mesure 捻 劉⁺, on a,-presque partout,

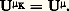On voit que 猪^K est la balayée de 猪 grâce à la remarque qui suit le théorème 5 et au théorème suivant.

Théorème 10 : Un borélien de Rⁿ est polaire si et seulement s’il est de-mesure nulle pour toute mesure 捻 劉⁺.

Norme et principe de Dirichlet

Soit 戮⁰ l’espace des fonctions numériques possédant un gradient fini continu de carré intégrable. Pour toute u 捻 戮⁰, on pose: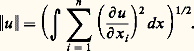

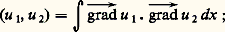L’application u 料 瑩u 瑩 est une semi-norme dans 戮⁰ associée au produit scalaire:

la condition 瑩u 瑩 = 0 équivaut à u constante.

Pour obtenir une norme on passe au quotient 戮 par la relation d’équivalence naturelle. La norme correspondante s’appelle la norme de Dirichlet . Par commodité de langage, on confond une fonction de 戮⁰ avec sa classe d’équivalence dans 戮.

Théorème 11 : Le sous-espace 流 des fonctions harmoniques est complet dans 戮.

Cela permet d’énoncer le principe de Dirichlet : pour toute fonction f 捻 戮, il existe une fonction harmonique u 捻 流 unique rendant minimum le nombre 瑩u 漣 f 瑩.

En effet, 流 étant un sous-espace complet, on obtient u par projection.

On peut ainsi résoudre le problème de Dirichlet dans les conditions suivantes: Soit 諸 un domaine borné de Rⁿ , n 閭 2, et f une fonction de 戮⁰ bornée dans 諸 et admettant un prolongement fini et continu à 諸 漣 (noté encore f ). La projection de f sur 流 est H^f size=1^諸. Si, de plus, 諸 est un domaine régulier, H^f size=1^諸 est l’unique fonction de 戮⁰ de norme minimale admettant en tout point la même limite que f .

En songeant à compléter l’espace 戮, J. Deny a été amené à introduire des fonctions appelées «BL précisées» ou «BLD», obtenues en précisant des fonctions introduites par Beppo Levi et Nikodym. Les classes d’équivalence de ces fonctions, par rapport à l’égalité presque partout à une constante près, forment un espace de Hilbert. On peut résoudre un problème de Dirichlet correspondant pour ces fonctions.

On peut faire le lien des fonctions BLD avec les potentiels U size=1^猪 d’énergie finie: Si 猪 捻 劉, alors U size=1^猪 est une fonction BLD et on a:

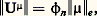où 﨏ⁿ est un coefficient numérique dépendant de n .

4. Théories axiomatiques et dérivées

Méthodes hilbertiennes

L’espace 劉 des mesures d’énergie finie n’étant pas complet, Deny, en 1950, introduit les éléments du complété en développant une théorie du potentiel dans Rⁿ , où le noyau est une distribution et le potentiel un produit de convolution de distributions (cf. DISTRIBUTIONS [Mathématiques]). Avec quelques restrictions, la théorie de Cartan peut être adaptée. Dans l’axiomatisation par Beurling et Deny des espaces de Dirichlet, on utilise le fait que la norme de Dirichlet est diminuée par les contractions normales: Si v varie moins vite que u , l’intégrale de Dirichlet relative à v est plus petite que l’intégrale de Dirichlet relative à u . Cette remarque, due à A. Beurling, permet de donner des démonstrations très courtes et très élégantes des résultats fondamentaux de la théorie du potentiel. Elle permet aussi de démontrer des théorèmes profonds de synthèse spectrale en analyse harmonique.

Théories axiomatiques sans noyaux

La théorie axiomatique de Brelot et de ses extensions ultérieures (Bauer, Constantinescu et Cornea) est inspirée d’une axiomatique probabiliste de Doob et fut précédée d’une tentative due à Tautz. Le principe en est le suivant.

Dans un espace 行 localement compact, on considère un faisceau d’espace vectoriel de fonctions numériques continues, appelées harmoniques (axiome 1). On suppose qu’il existe une base de domaines réguliers, c’est-à-dire tels qu’il existe une solution du problème de Dirichlet (axiome 2), et enfin (axiome 3) que tout ensemble filtrant croissant de fonctions harmoniques dans un domaine 諸 tend vers + 秊 ou une fonction harmonique. La théorie se développe considérablement si l’on ajoute le principe de domination (axiome D) comme nouvel axiome.

Les solutions dans un ouvert d’une équation du deuxième ordre de type elliptique à coefficients suffisamment réguliers vérifient les axiomes. Il en est de même, ce qui est plus difficile, pour des équations à coefficients discontinus (M^me Hervé). Cela apporte de considérables simplifications à l’étude directe de ces équations faites par Stampacchia.

En revanche, les solutions d’équations de type parabolique ne vérifient pas les axiomes 3 et D. C’est pourquoi Bauer modifia l’axiomatique précédente par l’introduction d’un nouvel axiome et l’affaiblissement de l’axiome 3, afin de contenir, dans les applications, les solutions d’équations de ce type.

Enfin, J. M. Bony est arrivé à caractériser de façon presque complète, en termes d’opérateurs différentiels, les théories axiomatiques du type Brelot, Bauer... dans Rⁿ .

Soit, par exemple, 流 une théorie axiomatique de Brelot telle qu’il y ait «suffisamment» de fonctions de classe 暈 size=1^秊. Il existe alors un ouvert dense dans lequel est défini un opérateur différentiel L à coefficients de classe 暈 size=1^秊 tel que toute fonction harmonique de classe 暈² vérifie Lu = 0 et même encore, au sens des distributions, si u n’est pas de classe 暈².

Théorie de Hunt et probabilités

Soit 行 un espace localement compact. On appelle noyau N une famille 猪^x de mesures dépendant mesurablement (en un sens à préciser) de x . On note 猪^x (E) = N(x , E). À toute f borélienne 閭 0, on associe:

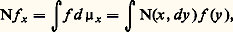également borélienne. On peut considérer N comme une application linéaire positive de l’ensemble des fonctions boréliennes positives dans lui-même. On peut donc composer deux noyaux. Si 益 est une mesure positive, on définit la mesure 益N par:

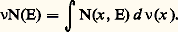L’exemple classique est le noyau:

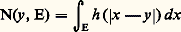dans Rⁿ . Ici N f est le potentiel newtonien de densité f et 益N est absolument continue par rapport à la mesure de Lebesgue, ayant comme densité le potentiel U size=1^益.

On dit que N satisfait au principe complet du maximum si, pour toute constante a 閭 0 et tout couple (f , g ) de fonctions positives universellement mesurables, la relation: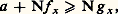

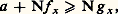pour tout x tel que g (x ) 礪 0, entraîne:

pour tout x 捻 行.

Avec certaines restrictions satisfaites dans les applications, G. A. Hunt montre qu’on peut associer à un noyau N, satisfaisant au principe complet du maximum, un semi-groupe P^t (défini pour t 閭 0, P^{s +t} = P^s 獵 P^t ) de noyaux, vérifiant des conditions de continuité à l’origine, tel que:

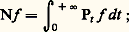cela lui permet de développer une théorie du potentiel purement probabiliste. On appelle excessives les fonctions f 閭 0 vérifiant:

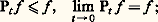en cas d’égalité, f est dite invariante . Quand f 閭 0 n’a pas de minorante invariante 閭 0 autre que zéro, f est appelée potentiel .

Dans les bons cas, P^t peut être interprété comme le semi-groupe de transition d’un processus de Markov. De tels processus sont appelés processus de Hunt. Dans le cas particulier du mouvement brownien, le générateur infinitésimal (dérivée à l’origine du semi-groupe) est l’opérateur , ce qui permet d’identifier les fonctions surharmoniques et les fonctions excessives. Il en est de même dans le cas général d’une théorie axiomatique du type Brelot. M^me Hervé a construit un noyau vérifiant des conditions qui permirent à P. A. Meyer de montrer l’existence d’un semi-groupe dont les fonctions excessives sont précisément les fonctions surharmoniques de la théorie.

Cette identification va beaucoup plus loin et permet d’interpréter en termes probabilistes les faits les plus importants de la théorie du potentiel: balayage, effilement, espace de Martin, etc. La théorie du potentiel est donc une source d’inspiration considérable pour les probabilistes qui s’occupent des processus markoviens.

Théorème de représentation intégrale

Les fonctions harmoniques positives dans un ouvert borné 諸 說 Rⁿ forment un cône convexe C; celles qui valent 1 en un point forment une base convexe compacte B (pour la convergence compacte) du cône et les fonctions minimales de cette base sont les éléments extrémaux de B. On peut aussi interpréter la représentation intégrale de Martin d’une fonction u 捻 B en disant que u est le barycentre d’une mesure 猪 portée par l’ensemble des points extrémaux (modulo une identification des éléments minimaux, c’est-à-dire extrémaux, de B avec les points de l’ensemble 臨¹ défini à la fin du chapitre 2).

Cette remarque a permis à G. Choquet de démontrer le théorème extrêmement profond qui suit.

Théorème. Soit C un cône convexe et B une base compacte de C. Si B est métrisable, tout x 捻 B est barycentre d’une mesure unitaire 猪 portée par l’ensemble des points extrémaux. De plus, si C est réticulé pour son ordre, 猪 est unique.

Si B n’est pas métrisable, le problème est beaucoup plus compliqué. En particulier, l’ensemble des points extrémaux n’est pas nécessairement mesurable.

On peut partir de ce théorème pour retrouver la représentation intégrale de Martin: c’est une méthode beaucoup plus simple. Ce théorème permet également de donner une représentation intégrale de Riesz dans les espaces harmoniques de Brelot (M^me Hervé, G. Mokobodski) et même, sous une forme moins satisfaisante, dans les axiomatiques affaiblies (Mokobodski).

Théorie de la capacité

Une capacité généralisée , au sens de Choquet, sur un espace topologique séparé X est une fonction réelle 暈 d’ensemble, définie sur toutes les parties de X; elle est croissante, descend sur les compacts et monte sur les ensembles quelconques. La capacité extérieure classique dans Rⁿ et les mesures extérieures sur X localement compact sont des exemples de capacité généralisée. Un ensemble A 說 X est dit capacitable si:

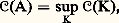la borne supérieure étant prise pour K parcourant l’ensemble des compacts contenus dans A.

Pour terminer, indiquons un théorème, dû à Choquet, qui est très utile en théorie de la mesure et en théorie des probabilités. Il nous faut pour cela donner quelques définitions: On dit qu’un ensemble dans un espace topologique est un K size=1^靖 si c’est une réunion dénombrable d’ensembles compacts; un K size=1^靖嗀 est un ensemble qui est intersection dénombrable de K size=1^靖; enfin, on dit qu’un sous-ensemble A d’un espace topologique séparé est analytique si A est l’image continue d’un K size=1^靖嗀 contenu dans un espace compact. Le théorème de Choquet s’énonce alors: Tout ensemble analytique contenu dans un K size=1^靖 est capacitable.

Encyclopédie Universelle. 2012.